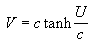
Direct calculations of acceleration at relativistic speeds from the Lorentz transform are complicated. I will present a set of concepts which simplify calculations for acceleration and travel at relativistic speeds.
The central concept in this scheme I have termed the Newtonian pseudo-speed. This is the speed that an accelerated object would be going if the universe operated only according to Newtonian physics. It corresponds to the integral of the infinitesimal speed changes in the accelerating object's own (changing) reference frame. It can be calculated simply by multiplying the object's acceleration by the time (as measured by the object's own clock). Along the same axis, Newtonian pseudo-speeds can be added directly, without worrying about relativistic velocity addition formulas. The Newtonian pseudo-speed is not limited by c.
The Newtonian pseudo-speed, U, is related to the actual speed, V by:
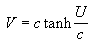
where tanh is the hyperbolic tangent function.
There is also a simple relationship between the Newtonian pseudo-speed and another quantity that I call the Einsteinian pseudo-speed (W). The Einsteinian pseudo-speed is a measure of the speed at which distances (as measured in the starting reference frame) go by as timed by the clock on the moving object. It allows for simple calculations of how quickly a spacecraft would seem to be going to a crew experiencing time dilatation effects. The Einsteinian pseudo-speed is related to the Newtonian pseudo-speed by:
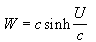
where sinh is the hyperbolic sine function.
Another interesting quantity is the time dilation ratio: the ratio (observed in the starting reference frame) between time intervals as measured by clocks in the starting reference frame to time intervals as measured by clocks in the moving object's reference frame. It is related to the Newtonian pseudo-speed by:
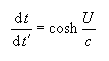
where cosh is the hyperbolic cosine function.
The above equations allow for calculation of speeds in non-accelerated objects, and the definition of the Newtonian pseudo-speed makes calculations of the time (as measured by the object's clocks) required for velocity changes easy (see the examples below). We also are interested in the time and distance in the starting reference frame required for speed changes. For a given acceleration a, the time (in the starting reference frame) required to change speeds is given by:
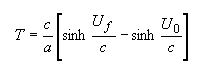
and the distance by:
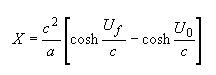
I will use c = 3e8 m/s in the examples to simplify the math. We begin with an ship that accelerates at 1000 m/s2 and starts out at rest relative to Earth. It accelerates for 600 000 seconds as measured by its on-board clocks (6.94 days). At the end of this time, the Newtonian pseudo-speed U = 6e8 m/s = 2c. The ship's actual speed is V = 0.96403c. The Eiensteinian pseduo-speed W = 3.6269c. This means that for each year that the ship travels at this speed (as measured by on-board clocks) it will travel between distances that the crew knows are 3.6269 light-years apart in the Earth's rest frame. Of course, in the ship's reference frame, the objects are moving at 0.96403c and the distances between them are contracted. The time dilation ratio is 3.7622, meaning that 3.7622 years pass on Earth for each year that the ship's clock counts off.
The acceleration from U = 0 to 2c took 600 000 seconds (6.94 days) according to the ship's clocks, but takes 1 088 058 seconds (12.59 days) according to the clocks on Earth [(3e8 m/s / 1000 m/s2) * (3.6269 - 0)]. The distance traveled (in the Earth reference frame) was 2.49e14 m (9.59 light-days) [( (3e8 m/s)2 / 1000 m/s2) * (3.7622 - 1)].
Now suppose the ship continues to accelerate at 1000 m/s2 for another 1 800 000 seconds (=20.82 days) of ship's time. The new U = 8c [(the starting U) + (1 800 000 s) * (1000 m/s2) = 2.4e9 m/s = 8c]. Now V = 0.99999977c, W = 1490.5c and the time dilation ratio is also 1490.5.
This acceleration takes significantly longer as measured by Earth clocks (3e8 m/s / 1000 m/s2)*(1490.5 - 3.6269) = 4.46e8 seconds = 14.13 years). The distance traveled (( (3e8 m/s)2 / 1000 m/s2) * (1490.5 - 3.76) = 1.34e18 m = 14.13 light-years) reflects the fact that the ship is moving at near light-speed throughout. After accelerating, the ship travels just over 4 light-years (as measured in Earth's reference frame) for each day of ship time (which is 4 years long according to Earth clocks).
Consider an object undergoing acceleration from a starting inertial reference frame O. The relativistic velocity addition formula is:
Let v be the speed of an object relative to reference frame O. We can relate the infinitesimal speed change in the object's own reference frame, du, to the speed change as viewed by an observer in frame O (dv) by:
which is derived from the velocity addition formula.
Solving for dv:
and simplifing:
We arrive at:
If we integrate both sides of the equation from zero to the final state of the object after acceleration, the upper bound of the left side will represent V, the actual speed of the object relative to frame O. The upper bound of the integral of the right side U represents the Newtonian pseudo-speed. It is the result of integrating infinitesimals which represent successive speed changes in the object's own reference frame and represents the speed the object would have if the universe had Newtonian physics.
Integrating:
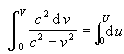
gives:
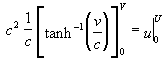
Substituting we have:
and rearranging:
Note that as U goes to infinity, V asymptotically approaches c, in accordance with the special relativity principle that no object can reach a speed of c. We can also check that U and V are equal when c goes to infinity (this is the check that the special relativity and Newtonian equations are consistent at low speeds).
The first few terms in the power series expansion of tanh x are:
and substitution gives:
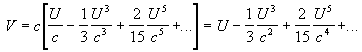
Now letting c go to infinity:
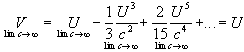
which checks.
The Einstienian pseudo-speed (W) is the speed at which distance as measured in frame O passes using a clock in the moving objects reference frame. Designating frame O as the unprimed frame and the object's frame as the primed frame,
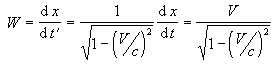
according to the Lorentz transformation.
Substituting for V:
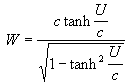
which simplifies to:
Since:
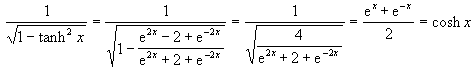
We can again check that the Newtonian and Einsteinian formulas agree at low velocity by using the power series expansion for sinh x:
Substituting:
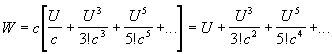
and letting c go to infinity:
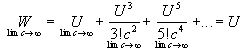
which checks.
To derive the time-dilation equation, we begin with the Lorentz transformation relating time flow in the primed and unprimed frames and substitute for V:
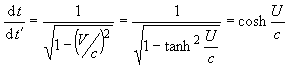
To determine the time it takes in the unprimed frame for a speed change, we substitute the equation for uniform acceleration in the primed (object) reference frame:
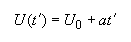
into the time dilation equation and rearrange to isolate all t´ terms on the right:
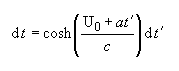
Intergrating:
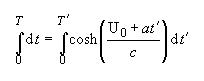
we have:
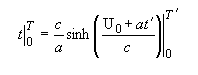
Substitution gives:
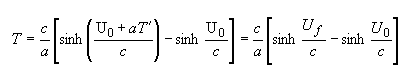 where
where
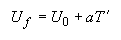
To determine the distance in the unprimed frame required for a velocity change, we start with the formula for the velocity as a function of t´:
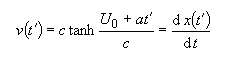
We would like to isolate t´ terms on one side, and dx on the other, followed by integration. First the dt term must be eliminated. Multiply both sides of the velocity formula by the time dilation ratio:
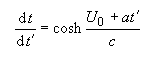
Giving:
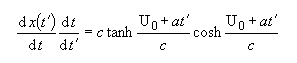
Which simplifies to:
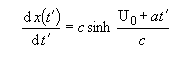
Multiplying both sides by dt´, and i ntegrating from the start of the acceleration to its end:
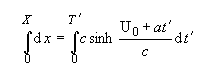
and substituting:
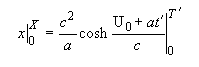
gives the final result:
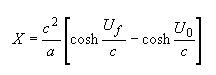 where
where
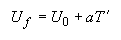
Up to the
science in science fiction page.
Up to the science fiction page.
[Home] [Comp] [SF] [Med/Bio] [Other Sci] [Personal]